Chapter 1: The Concept of Integration by Parts

Integration by parts is a valuable tool within calculus, utilized primarily for determining antiderivatives of the product of two functions. But what is the origin of this formula?

The principle behind integration by parts revolves around finding the antiderivative of the product of two functions. To begin, we need to explore the derivative of a product of functions, which leads us to the product rule.

The derivative ( u' ) of a function ( u(x) ) can be expressed as follows:

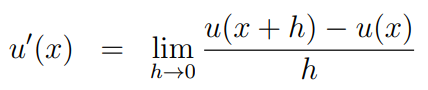
According to the product rule, the derivative of the product ( u cdot v ) can be written as:

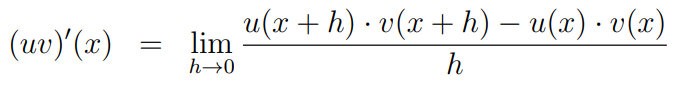
In mathematics, it’s common to introduce a helpful term and then subtract it, effectively adding zero to the equation.

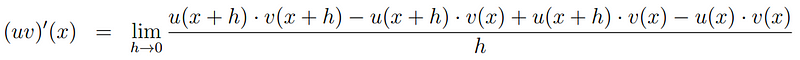
We can then break this expression down further.

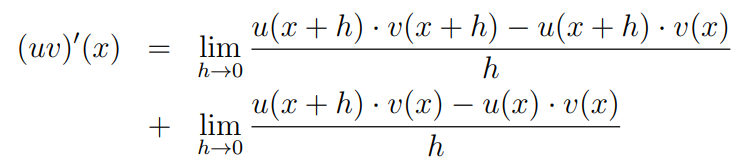
Next, we factor out the common elements from the numerator of each fraction.

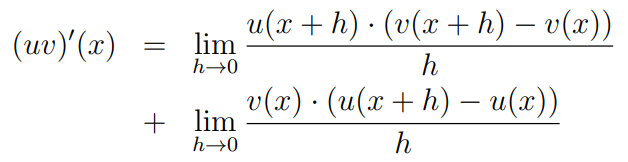
By the property of limits, the limit of a product equals the product of the limits, allowing us to separate the components:

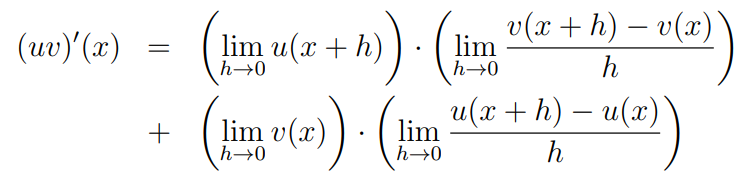
The limits on the left-hand side yield the functions ( u(x) ) and ( v(x) ), while those on the right represent the derivatives of each function.

Evaluating these limits results in:

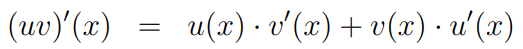
This is the familiar product rule that we often use in calculus.

To derive the integration by parts formula, we can rearrange the product rule:

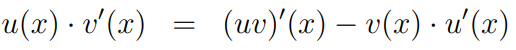
We then integrate both sides with respect to ( x ):

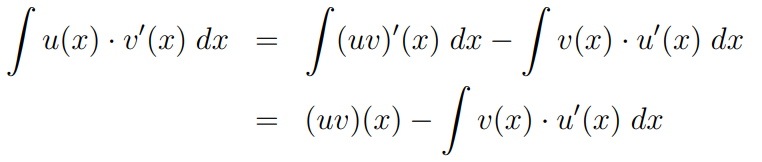
The expression ( (uv)' ) simply integrates to ( uv ), leading us to the integration by parts formula.

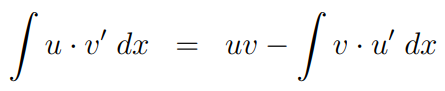
This derivation is essentially a rearrangement of the product rule followed by integration. One might wonder if a similar method could be applied using the quotient rule. While theoretically possible, it could result in a complex series of functions in the initial integral.

Challenge: In the process of deriving the product rule, I added and subtracted ( u(x + h) cdot v(x) ). Could I have introduced zero in another way? If so, what would be the reasoning behind it?