Math Challenge Recap: Weekly Game 15 Results and Insights
Written on
Weekly Math Games Overview
The 15th edition of our Weekly Math Games has proven to be quite a challenge, with only four participants submitting entries this time. Currently, the scoring system is somewhat improvised, but I plan to refine it in future games.
Let’s extend a hearty congratulations to our winners this week! 🎉
- 1st Place: Wotsit with 7 points 🏆
- 2nd Place: Alfredo Esposito with 5 points 🥈
- 3rd Place: Carl Reiner Holdt with 3 points 🥉
- Other Participants: Vivek Amar with 1 point 🏅
A special shoutout goes to Alfredo Esposito for discovering a superior upper bound than what was originally posed. He analyzed the function ( frac{1}{1 + x^2} ) and cleverly utilized a trapezoidal approximation, yielding an upper bound of approximately 0.279, which is lower than the intended upper limit of about 0.292.
Understanding the Solution
In this challenge, we are examining a definite integral. The bounds for our investigation are set between 1 and 2, providing a natural starting point with the interval ([1, 2]).
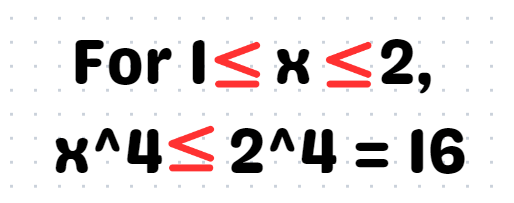
You can verify this by substituting different values for ( x ). When we add one to both sides of the equation, we find:

Remember, when we take the reciprocal, we must flip the inequality sign.
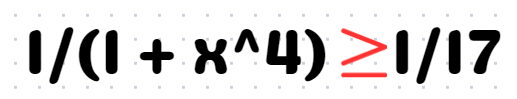
Given this relationship, the same holds true when we apply the definite integral from 1 to 2. This concept is rigorously explored in university-level real analysis courses!
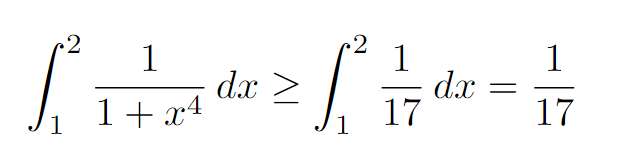
Integrating the constant ( frac{1}{17} ) gives us ([x/17]) with the limits applied; thus, substituting yields ( frac{2}{17} - frac{1}{17} = frac{1}{17} ). This establishes our lower bound.
Next, we need to identify the upper bound, starting from the following expression.
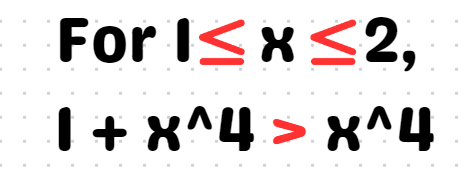
This step should be straightforward. Again, utilizing the principle of reciprocal relationships, we can flip the inequality sign.
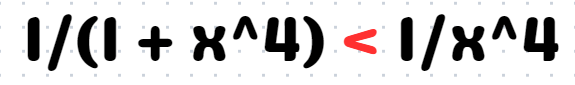
Then, we apply the definite integral as follows:
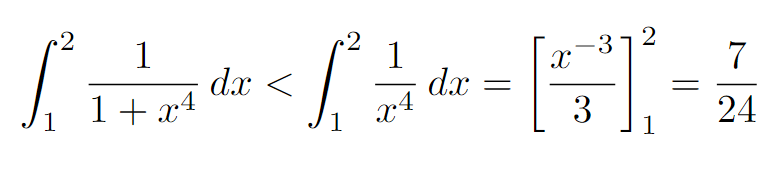
This yields our upper bound. Compiling all our results, we arrive at:
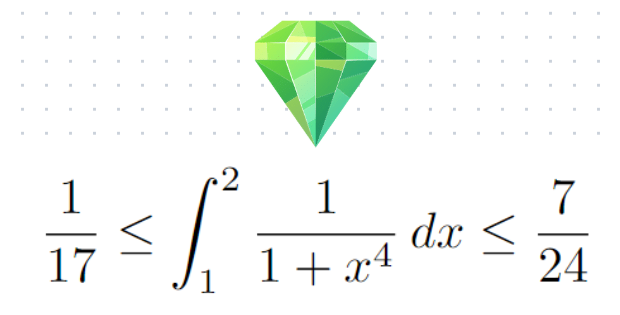
And there you have it! How did you fare in the 15th Math Games? Looking forward to next week’s challenges! 🎊

The video "Can you prove this?" challenges viewers to engage with mathematical proofs and explore complex problems in mathematics.
In the video titled "Prove this," participants are encouraged to tackle challenging mathematical proofs and enhance their problem-solving skills.