The First Encounter

When my father was a high school student, he was investigating strategies to enhance his odds in betting. During his research, he stumbled upon a remarkable symmetrical arrangement of numbers that emerged during his calculations.

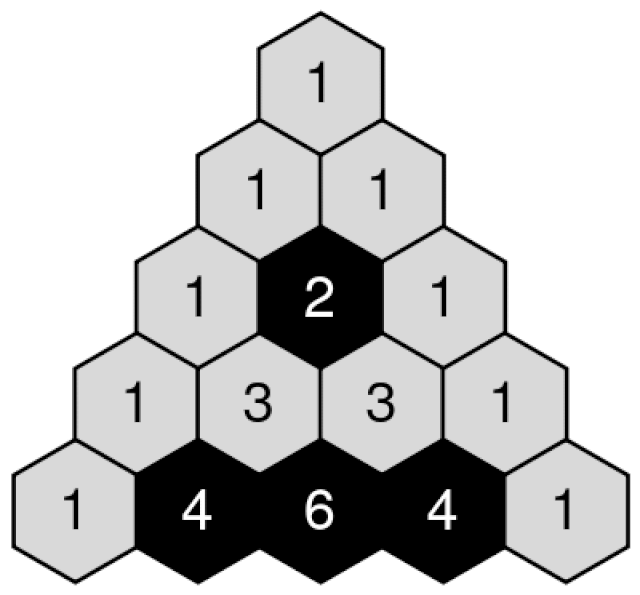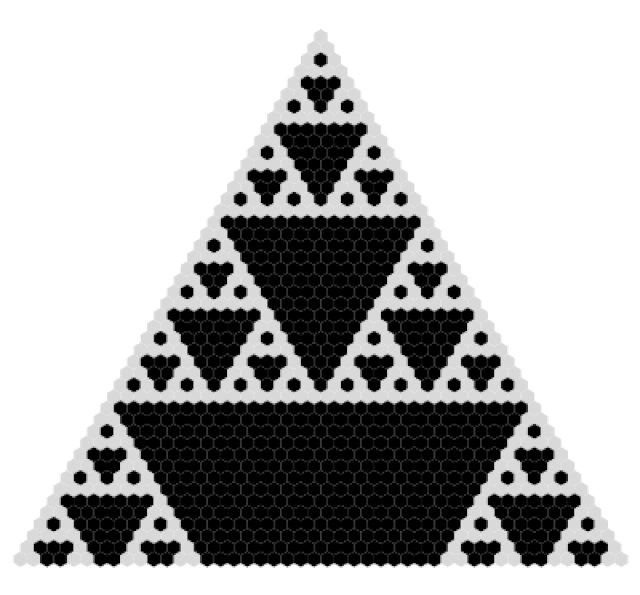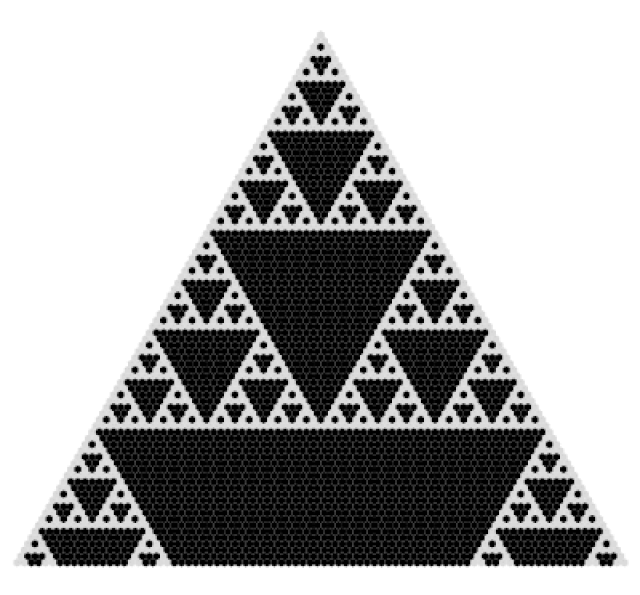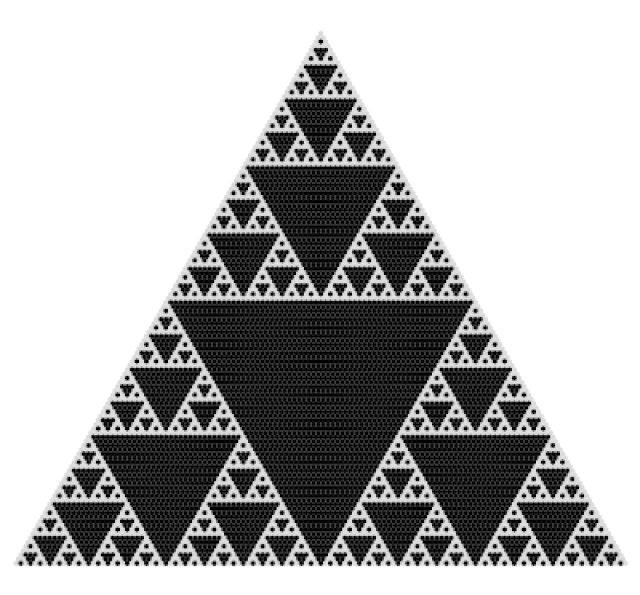
He discovered that these numbers formed a unique pattern when arranged in a triangular formation. Eager to share his finding, he rushed to his math teacher, who instantly recognized the well-known structure. The triangle he uncovered is depicted below:

This triangle continues infinitely, with each new row created by summing the two numbers directly above it (considering the absent spots as zeros). Despite its straightforward construction, this shape reveals remarkable insights.

Little did my father realize that this mathematical marvel had been examined for over a millennium across various cultures. In Iran, it’s referred to as Khayyam's triangle, while in China, it's known as Yang Hui's triangle. In Western contexts, it is predominantly called Pascal's triangle, named after Blaise Pascal, who explored it in relation to probability theory.

The numbers in this triangle are called binomial coefficients, which represent the different ways to select k items from a set of n. For instance, on the fourth row and second position (counting from zero), there are 6 ways to choose 2 items from 4.

You might also remember from algebra that the expansions (a + b)² = a² + 2ab + b² and (a + b)³ = a³ + 3ab² + 3a²b + b³ correspond to the coefficients in the second and third rows of Pascal’s triangle. This correlation is a reflection of the binomial theorem.

Geometry and Numbers

The most elementary patterns within the triangle consist of the 1s that line its edges. Parallel to these, you'll find the sequence of natural numbers: 1, 2, 3, 4, 5, … and the adjacent line showcases the triangular numbers: 1, 3, 6, 10, 15, 21, …

These numbers can be arranged in a triangular formation, obtained by summing the initial natural numbers. For example, 10 can be expressed as 10 = 1 + 2 + 3 + 4, which represents the total number of balls in the following triangular layout:

The next series parallel to the edge in Pascal's triangle comprises tetrahedral numbers, starting with 1, 4, 10, 20, … These numbers correspond to the count of balls arranged in a tetrahedral formation (a pyramid with a triangular base).

Powers and Patterns

One fascinating aspect of this triangle is that each direction reveals a distinct pattern. For instance, if you sum the numbers in each row, you arrive at the powers of 2:

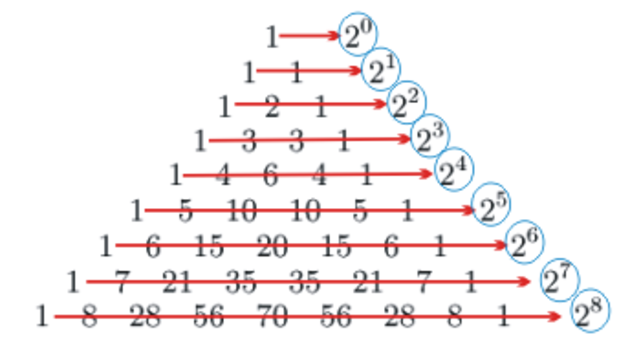
The corresponding formula for those interested is:

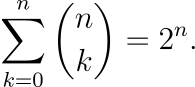
This connection is evident from the binomial theorem. Another intriguing pattern arises when treating each coefficient as a number: you can observe sequences like 1 = 11¹, 11 = 11¹, 121 = 11², 1331 = 11³, and so forth. However, there’s a caveat: coefficients must be treated as multiplied by 10^k and summed, which aligns with earlier “numbered rows” but diverges when coefficients exceed 9.

The Hockey Stick Identity

An interesting property occurs when you sum numbers along a diagonal and shift one step sideways; this results in the sum of the diagonal. This phenomenon is illustrated in the following image:

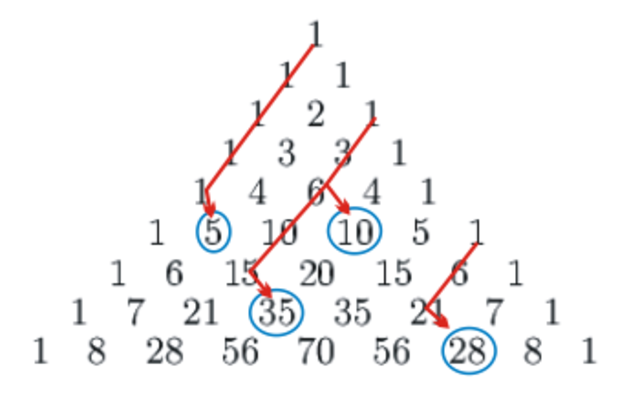
If you follow the red lines, you will find that summing these numbers yields the subsequent number perpendicular to the diagonal—a fun exercise to prove!

Fractals and Their Fascination

A particularly astonishing pattern emerges when examining Pascal’s triangle modulo 2 (differentiating between even and odd numbers). By categorizing these numbers by color, a captivating fractal pattern unfolds as we explore additional rows.

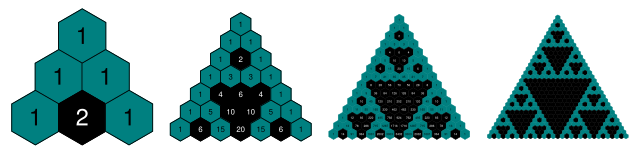
This formation is recognized as the Sierpiński triangle, a renowned fractal. You can experience its beauty through the following animation:

Exploring Binary Numbers

If we take the values from Pascal’s triangle and reduce them modulo 2 (where odd numbers become 1s and even numbers become 0s), we obtain a version of the Sierpiński triangle:

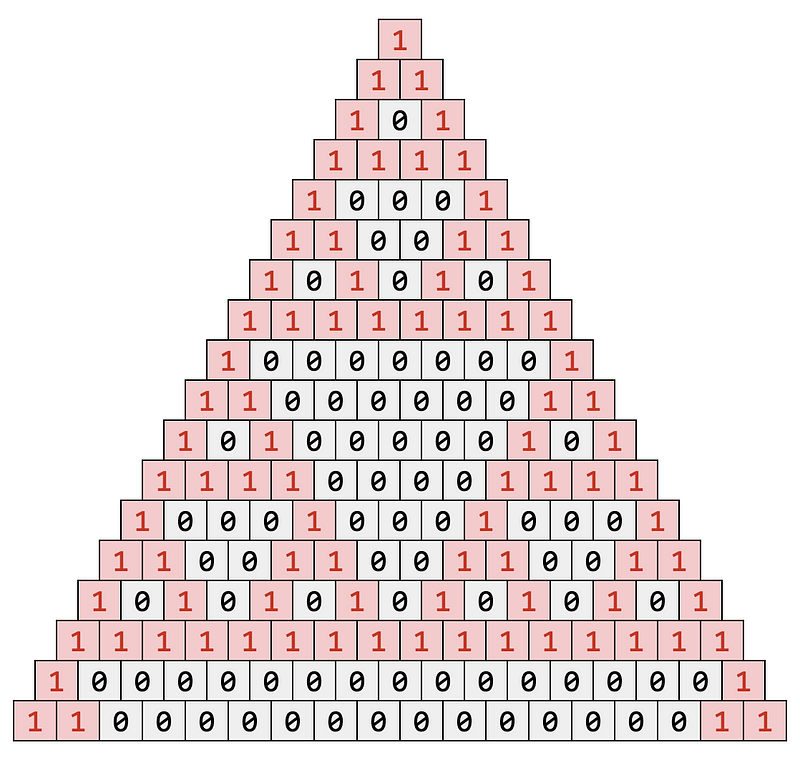
When interpreting each row as a binary number, an intriguing sequence arises: 1, 3, 5, 15, 17, 51, 85, 255, 257… At first glance, this sequence seems random; however, if we factor each number into primes, we see:

13515 = 3 × 51751 = 17 × 385 = 17 × 5255 = 17 × 3 × 5257

The pattern reveals that each subsequent number is generated by multiplying a combination of previous numbers. The unbroken numbers are prime, specifically Fermat primes of the form 2^(2^n) + 1. Nevertheless, it remains uncertain whether this sequence contains infinitely many primes—a question yet to be resolved.

The Fibonacci Connection

The Fibonacci numbers are celebrated in the realm of natural numbers, beginning with 1, 1, 2, 3, 5, 8, 13, 21, … where each number is the sum of the two preceding ones. While this sequence merits its own discussion, it is worth mentioning that it is closely associated with the golden ratio φ:

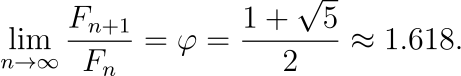
Remarkably, the Fibonacci sequence is also present in Pascal’s triangle. Specifically, if you sum specific diagonals, you will uncover the Fibonacci numbers:

This relationship is astonishing and can be demonstrated using binomial coefficients—a rewarding challenge to prove without induction!

Final Thoughts

The patterns hidden within Pascal's triangle are virtually limitless, and mathematicians continue to discover new ones. The allure of this mathematical marvel never ceases to amaze.

Who knows what surprises await in the millionth row? My father first introduced me to this subject long ago, and I wonder if he will find something new in this exploration.

What pattern in Pascal’s triangle intrigues you the most? Feel free to share your thoughts in the comments!

Thank you for joining me on this mathematical journey. If you enjoy reading articles like this, consider joining Medium for full access to more insightful content.

Further Exploration

Discovering Hidden Patterns in Pascal's Triangle (ft. Marc Evanstein / music.py) explores the fascinating numerical sequences within this triangle.

Top 10 Patterns in Pascal's Triangle provides an engaging look at the most intriguing structures within this mathematical landmark.