Exploring Euclidean Geometry with Python: A Practical Guide
Written on
Chapter 1: Introduction to Scientific Python
In this series, we delve into the practical applications of the Python scientific stack for tackling real-world challenges. Mastering these tools takes consistent practice, and this series aims to guide you through solving both common and unusual problems using libraries such as NumPy, SymPy, SciPy, and matplotlib.
Today's Challenge
Today, we will focus on creating geometric shapes using matplotlib while also leveraging vector algebra with SymPy. The objective is to demonstrate Thales' theorem without traditional pen and paper, relying solely on Python's scientific libraries. Although the theorem itself is straightforward, the emphasis here is on efficiently utilizing the Python stack.

Thales' Theorem Explained
Thales' theorem asserts that if a triangle's one side is the diameter of a circle, and the third point lies on the circumference, then the angle opposite to the diameter is a right angle. To visualize this scenario, we will plot it using a Jupyter notebook. Below is a plotting script with comments for clarity.
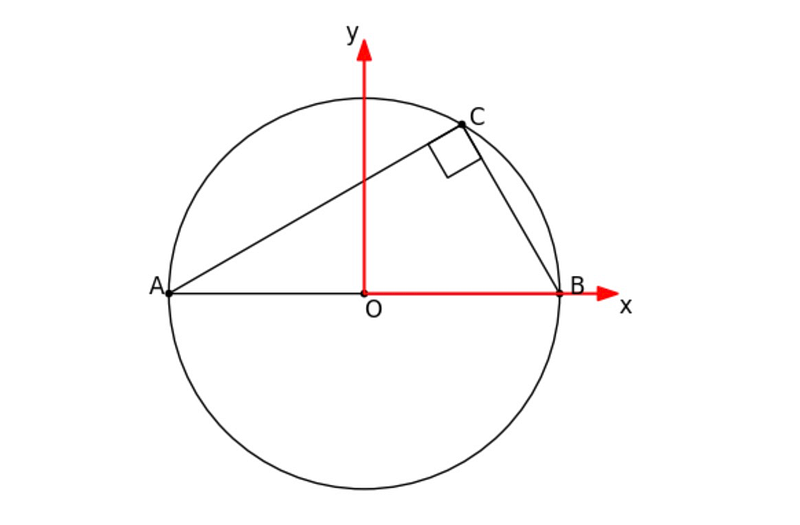
To prove Thales' theorem using vector algebra, we will establish a coordinate system centered at the circle's origin. We will also add coordinate axes to our plot for better understanding.
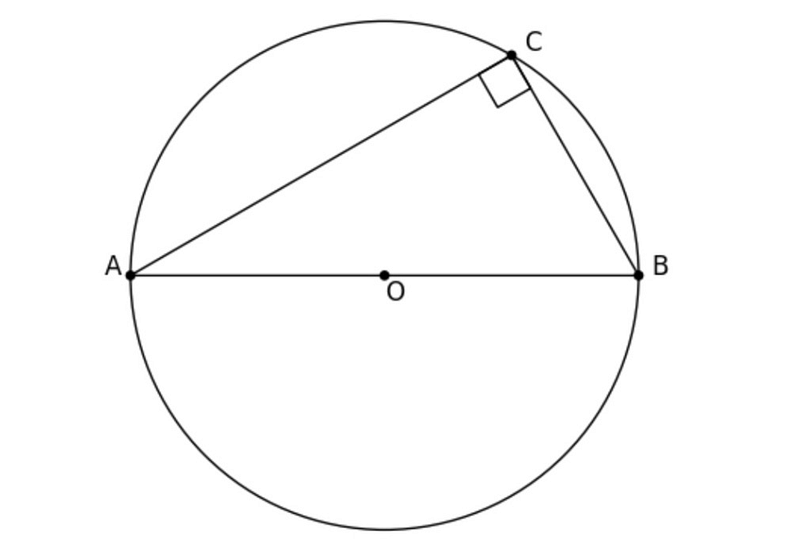
With our coordinate system in place, we can now plot the position vectors for points A, B, and C.
Using SymPy for Proof
For the proof, we will define the polar angles for points A and B as 0 and θ, respectively, while allowing the angle at point C to be arbitrary. The radius of the circle will also be treated as a variable. We will define the necessary symbols and vectors as follows:

Our goal is to establish that the angle at point C is indeed a right angle. To do this, we will need to calculate the sides AC and BC.

Next, we compute the scalar product:
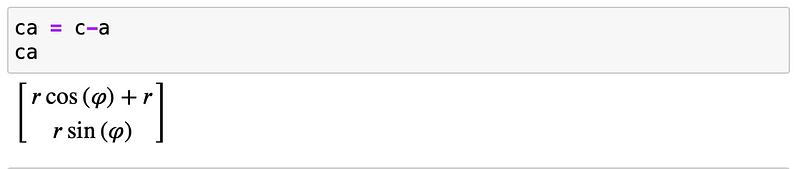
Since the scalar product is zero, we can conclude that the angle at point C is a right angle.
Chapter 2: Practical Applications and Further Exploration
This video titled "Euclidean Distance - Practical Machine Learning Tutorial with Python" explores how to compute distances in Euclidean space using Python, providing practical examples and coding insights.
In this follow-up video, "Euclidean Distance: Math, Applications and Code #SoME3," the mathematical foundations of Euclidean distance are discussed alongside its real-world applications and implementation in Python.