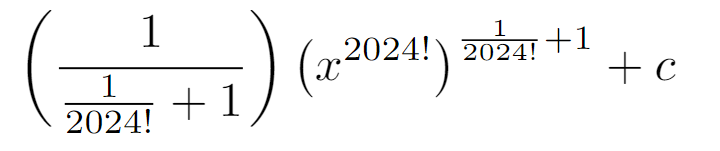A Unique Approach to Solving a Complex Integral: 2024!
Written on
Chapter 1: Introduction to the Integral Challenge
This intriguing problem draws inspiration from a comment made by Mackerethsamuel on one of my previous posts. He shared an insightful method for addressing these types of integration challenges. His suggestion was to reframe the expression as (x²)^(1/2) and integrate concerning x², resulting in a factor of 2/3.
Can you apply a similar strategy to today’s integral conundrum? I encourage you to pause here, take your pen and paper, and give it a try. Once you’re ready, continue reading to discover the solution!
This paragraph will result in an indented block of text, typically used for quoting other text.
Section 1.1: Understanding Dummy Variables
In calculus, the variable x in the differential dx is often referred to as a dummy variable, which means you can substitute it with any symbol you choose!
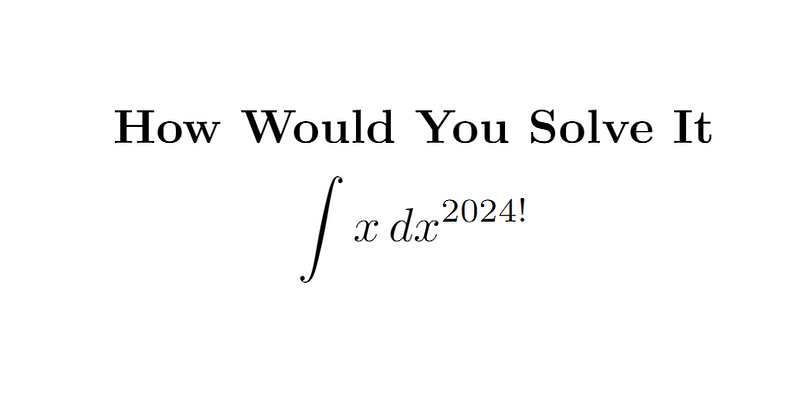
Here, x^(2024!) serves as our dummy variable. This is the term we are integrating. So, how do we approach this integration?
Reflect on how we can express x in terms of the variable we are integrating. It turns out, this is relatively straightforward!
Section 1.2: Rewriting the Integral
This crucial observation allows us to manipulate our integral into a more manageable form.
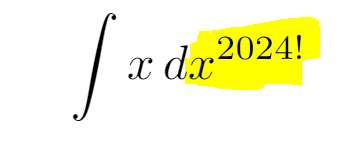
If you’re still uncertain, I utilized u as a substitution. With the integral on the right, we can now apply the reverse power rule!
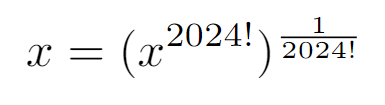
By adding 1 to the exponent and multiplying by its reciprocal, we can illustrate the integral's transformation. Next, we just need to rewrite u back in terms of x.
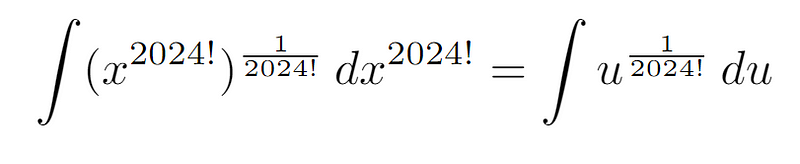
Don’t overlook the constant c, which is vital in our final expression.
Finally, let's clean up our notation:
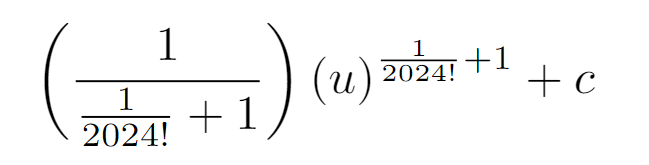
Isn't this fascinating? What were your thoughts throughout this process? Feel free to share in the comments; I'm eager to hear your insights!
Chapter 2: Engaging with Further Resources
In the first video titled "This is one of the coolest integrals ever solved," we delve deeper into intriguing integral solutions and methodologies.
The second video, "Hint: 2024 will appear in the solution," provides additional hints and strategies relevant to the concept explored in this article.
Thank you for engaging with this content! If you found it helpful, please consider sharing it and clapping for the article.