Chapter 1: Introduction to Linear Regression

Linear regression is a statistical technique that utilizes a regression equation to create a line that predicts values based on input data.

In this context, the dependent variable (y) is the predicted value, while the independent variable (x) is the influencing factor. The slope of the regression line is denoted as b, and a represents the y-intercept.

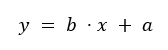
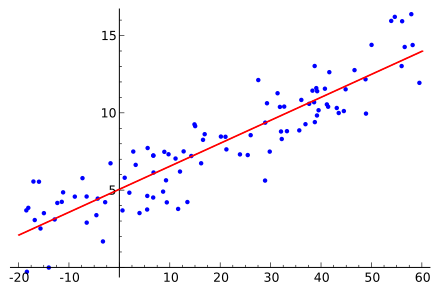
The blue dots illustrate individual data points, while the red line signifies the calculated regression line. The slope (b) is determined using the following formula:

Here, s represents the standard deviation, and r denotes the correlation coefficient.

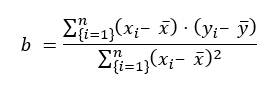
To compute the y-intercept (a), the previously calculated slope (b) is necessary.

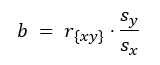
Linear regression relies on the assumption that there is a linear correlation between the variables, aiming to find the optimal straight line that fits the data points. This fitting process involves minimizing the residuals, which are the discrepancies between the actual values and the points on the regression line. The objective is to minimize the sum of squared residuals to achieve the best fit.

In the video “Stanford CS229: Machine Learning - Linear Regression and Gradient Descent | Lecture 2 (Autumn 2018),” the concepts of linear regression are further explored, providing insights into gradient descent and its application in machine learning.

Section 1.1: Multiple Linear Regression

Simple linear regression addresses only one independent variable's impact on the dependent variable. When multiple independent variables are involved, multiple linear regression becomes necessary.

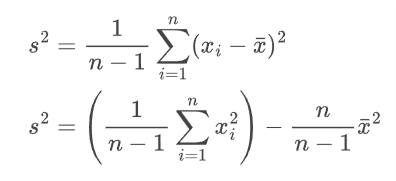
The formula for multiple linear regression is constructed similarly:

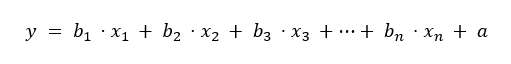
Here, x_n represents the n-th independent variable, while y is the predicted dependent value. The slope (b) and intercept (a) are also included in this equation.

To gain a deeper understanding of the evaluation of regression results, consider reviewing metrics that assess model accuracy and performance.

The video “Why Linear regression for Machine Learning?” elaborates on the significance of linear regression in the broader context of machine learning, enhancing comprehension of its utility.

Chapter 2: Conclusion

Regression analysis serves as a vital statistical method for examining relationships among variables. While simple regression focuses on the impact of one independent variable on a dependent variable, multiple regression takes into account the effects of various independent variables. Simple regression acts as an introductory tool for modeling relationships, whereas multiple regression provides a framework for more intricate analyses by considering multiple influences simultaneously. Both methodologies are indispensable for predictive modeling and hypothesis testing, making them crucial for professionals in applied computer science.