Solving the 2011 Indonesia Regional Olympiad Geometry Challenge
Written on
Chapter 1: Problem Statement and Setup
In this geometry challenge, we are tasked with analyzing a rectangle ABCD where O represents the intersection of the diagonals. A point E is located on the line extending BA from B through A, ensuring that AE equals AO. Additionally, point Z lies along the extension of diagonal DB from D through B such that BZ is equivalent to BO. Given that triangle EZC is equilateral, our goal is to demonstrate that BC equals AB multiplied by the square root of 3, and that segment EO is perpendicular to ZD. For reference, please consult the Theorem Grid for the relevant theorems utilized throughout this proof.
Introducing: The Theorem Grid
Theorems on Geometry Thus Far

From the stated problem and the accompanying diagram, it is clear that several segments of equal length are involved. This suggests the presence of multiple similar triangles. Since rectangles are a type of parallelogram, Theorem 1.9 guarantees that AO = BO = CO = DO. Given that AE equals AO and BZ equals BO, we derive that AE = OC and AC = OZ. Additionally, because triangle EZC is equilateral, we conclude that CE = ZC. By synthesizing these findings and applying Theorem 1.1, we can assert that triangle ECA is similar to triangle CZO.
Section 1.1: Analyzing Angles
We observe that angle OAB measures 60 degrees, leading us to conclude that triangle AOB is equilateral, and thus angle BOA is also 60 degrees. Moreover, since AE equals AO, we can once again utilize Theorem 1.3.
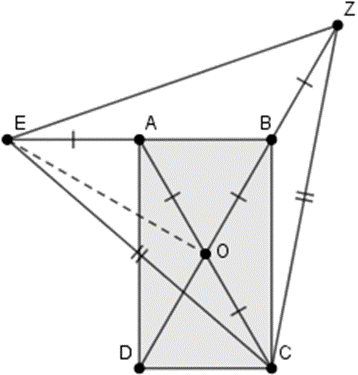
This reasoning establishes that angle BOE equals angle BOA plus angle AOE, resulting in 60 degrees plus 30 degrees, which equals 90 degrees. This confirms that EO is perpendicular to ZD.
Subsection 1.1.1: Utilizing Trigonometry
To demonstrate that BC equals AB multiplied by the square root of 3, we must connect the known angles to the lengths of the segments. This is where trigonometry comes into play! Notably, triangle ABC is a right triangle at point B.
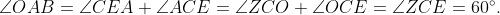
Endnote
The proof that angle BOE equals 90 degrees can be accomplished through various methods. One alternative approach is to observe that triangle BOE is congruent to triangle ABC, establishing that angle BOE equals angle ABC, which is 90 degrees. Additionally, the function representing sine over cosine is known as "tangent," or "tan" for short. However, we have not previously introduced this terminology in our discussions.
If you're interested in visual explanations and further insights, check out the following videos:
This video showcases a challenging Math Olympiad problem from Indonesia, guiding viewers through the solution process.
Here, we explore Problem #4 from the 1990 International Mathematical Olympiad, providing detailed explanations and strategies.