Chapter 1: Introduction to the Paradox

The puzzling concept of Gabriel's Horn presents a fascinating mathematical mystery. Often regarded as one of the "wonders of mathematics," it is a topic that many educators may avoid introducing to less experienced students, possibly due to fear of overwhelming them. This intriguing paradox has its roots in advanced mathematical analysis, but why is it often kept under wraps?

Perhaps many mathematics instructors are simply unfamiliar with such topics, or they worry that revealing these complexities might deter students. Regardless of the reason, the allure of this mathematical curiosity is undeniable.

To begin unraveling this paradox, consider a horn-shaped object that can hold paint but cannot have its surface painted. This situation leads us to the intriguing mathematical entity known as Gabriel's Horn. Specifically, this 2-dimensional shape possesses a finite volume while having an infinite surface area.

In this article, we will delve into the mathematics that defines this peculiar shape.

Chapter 2: Historical Background

Gabriel’s Horn, first discussed by Evangelista Torricelli in 1643, draws its name from the Christian belief that the archangel Gabriel will sound a horn on Judgement Day. This analogy is fitting, given the stir that this concept created in mathematical circles.

The horn is created by revolving the curve of the function f(x) = 1/x (for x ≥ 1) around the x-axis. The resulting shape is depicted below.

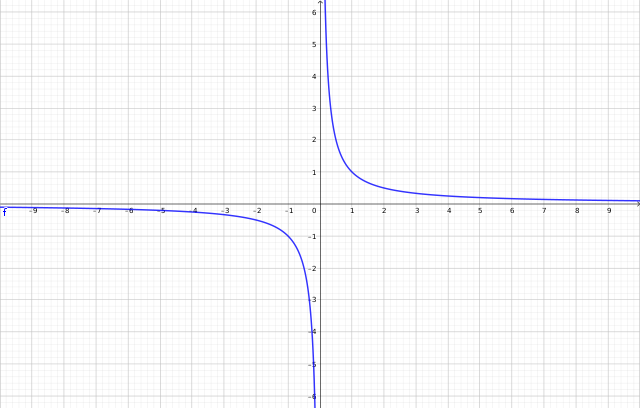
Chapter 3: Exploring Area, Volume, and Improper Integrals

Before we proceed with the calculations, we need to establish the formulas for determining volume and surface area via revolution.

Volume Calculation

To find the volume, we sum infinitely thin cylinders with a radius of f(x) and a width of dx. The area of a circle is πr², leading us to the formula for the volume of these cylinders as πf(x)²dx. This summation can be expressed as an integral, where we let dx approach zero.

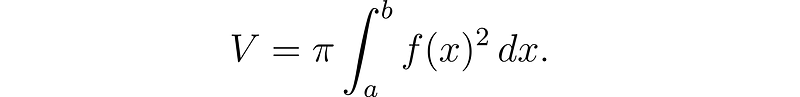
Surface Area Calculation

Calculating the surface area requires determining the length of the graph of f before revolving it. Using the Pythagorean theorem, we define small increments in the x and f directions, creating a right triangle that approximates the graph's length.

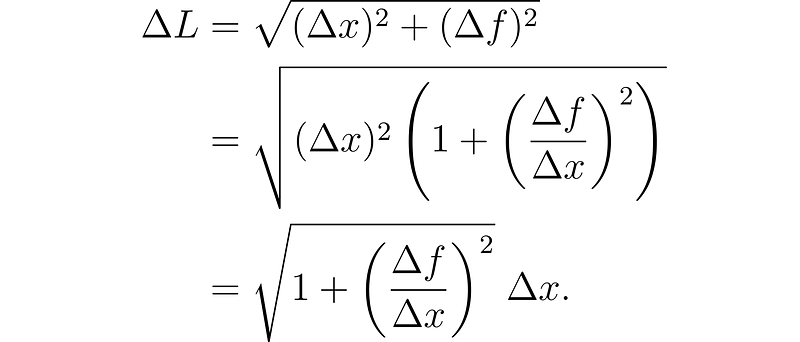
To find the surface area of the resulting slanted cylinder, we recognize that the circumference is given by 2πf(x).

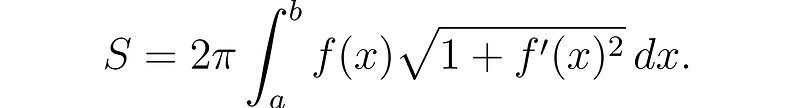
Understanding Improper Integrals

Improper integrals are used when the antiderivative is undefined at one or both bounds or when the limits extend to infinity. In this case, we define the integral using limits.

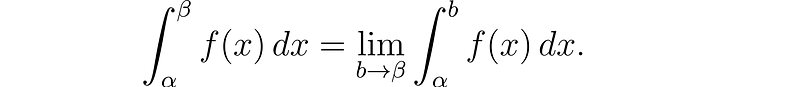
Chapter 4: Calculating the Volume and Surface Area

Now, let’s compute the volume of Gabriel's Horn by substituting f(x) = 1/x into the volume formula over the interval from 1 to ∞.

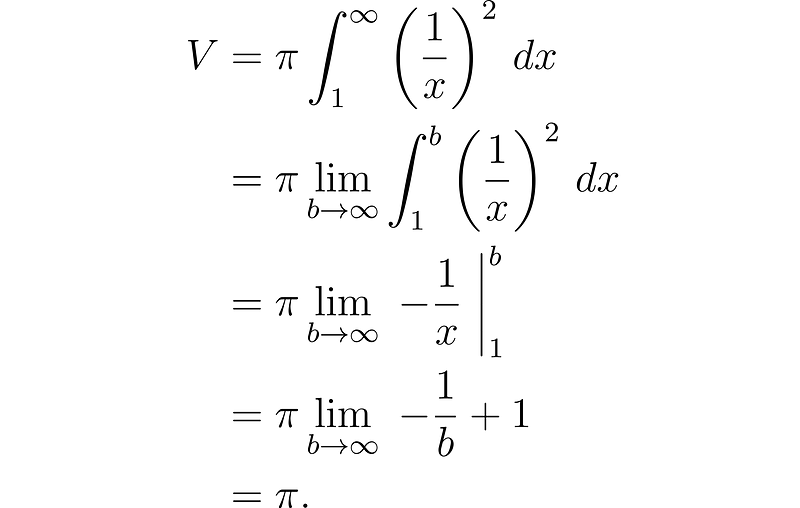
Astoundingly, Gabriel's Horn can contain exactly π units of paint!

Next, we turn to the surface area calculation, denoting it as a function of the length of the horn.

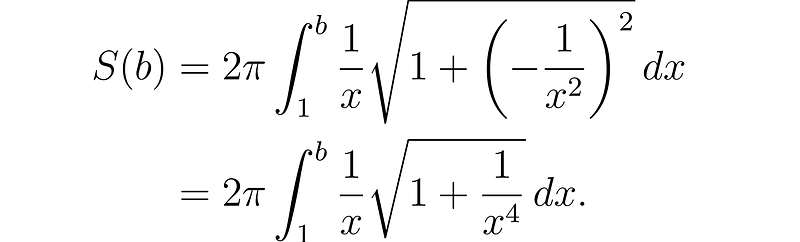
This integral can be complex, but recognizing that x runs from 1 to ∞ allows us to establish a lower bound for the integral.

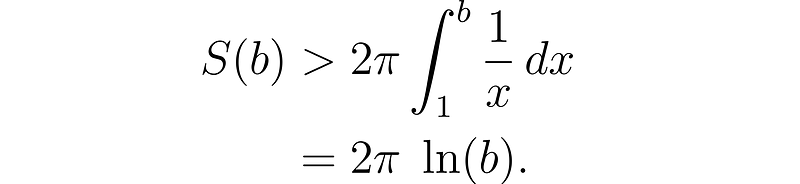
Taking the limit indicates that the surface area is infinite.

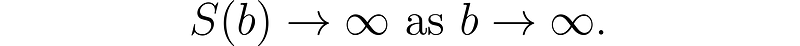
Chapter 5: Philosophical Reflections

The idea of a shape with finite volume and infinite surface area raises intriguing philosophical questions. While it seems paradoxical, this phenomenon highlights the differences between the mathematical and physical realms.

In reality, paint in the physical world cannot be infinitely divided; it consists of discrete molecules. Thus, any paint applied to a surface will possess a thickness, leading to a non-zero volume. The discrepancy between mathematical abstraction and physical reality illustrates why this paradox exists.

Consider this: can a shape exist with finite surface area and infinite volume? If so, can you provide proof? Share your thoughts in the comments!

If you enjoyed this exploration of mathematical curiosities, consider joining Medium for more fascinating articles.

In this video, titled "Gabriel's Horn Paradox," Numberphile delves deeper into the mathematical intricacies of Gabriel's Horn, providing visual explanations and insights.

The second video, "The Painter's Paradox," further explores the implications of this paradox in a broader context, enhancing your understanding of its significance in mathematics.