A Fresh Perspective on a Newly Discovered Math Equation
Written on
Chapter 1: Unraveling the Discovery
In the realm of mathematics, I have come across three significant equations that I would like to share. These equations pertain to an up-down parabola, which can be understood through the lens of their intersections and properties.
These equations provide a framework for examining the relationships between intersection points and the focus of the parabola.
Section 1.1: Understanding the Equations
When a line with slope ( m ) intersects a parabola characterized by a parabolic constant ( a ), the distance ( d ) between the points of intersection is divided by the focus into two segments: ( d_1 ) and ( d_2 ).
The first equation is straightforward; it states that ( d ) is simply the sum of ( d_1 ) and ( d_2 ). The second equation allows for the calculation of the parabolic constant ( a ) based on the values of ( d_1 ) and ( d_2 ). A positive ( a ) indicates an upward-opening parabola, while a negative ( a ) indicates a downward-opening one.
Now, the third equation introduces a notable distinction with the inclusion of a square root. This means that although the slope ( m ) can be computed using ( d_1 ) and ( d_2 ), achieving a rational ( m ) requires that the product of ( d_1 ) and ( d_2 ) be a perfect square.
Section 1.2: The Significance of Perfect Squares
To illustrate this, let's consider an example. We can assign ( d_1 = 2 times (5/3) ) and ( d_2 = 2 times (3/5) ). Here, the fractions ( 5/3 ) and ( 3/5 ) are reciprocals, yielding a product of one—a perfect square. Multiplying each by 2 gives us ( d_1 = 10/3 ) and ( d_2 = 6/5 ).
Next, we can calculate ( d ), ( a ), and ( m ) using our equations:
Calculating ( d ):
( d = 10/3 + 6/5 = 68/15 )
Finding ( a ):
( a = frac{(10/3 + 6/5)}{(4 times (10/3) times (6/5))} = frac{68/15}{240/15} = frac{68}{240} = frac{17}{60} )
Determining ( m ):
( m = frac{(10/3 - 6/5)}{(2 times sqrt{(10/3) times (6/5)})} = frac{32/15}{2 times 2} = frac{8}{15} )
Thus, if we define our parabola as ( y = frac{17}{60}x^2 ) and our line as ( y = frac{8}{15}x + frac{15}{17} ), the distance ( d ) between the intersection points is indeed ( 68/15 ), with ( d_1 = 10/3 ) and ( d_2 = 6/5 ). The focus of our parabola is located at ( (0, frac{15}{17}) ) since ( p = frac{1}{4a} = frac{15}{17} ).
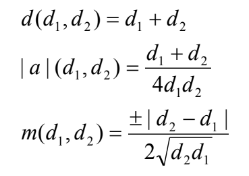
Chapter 2: Practical Applications
As we analyze this problem further, it becomes evident that we can develop exercises suitable for intermediate algebra students. For instance, we could challenge them to solve the system of equations relating to the line and the parabola.
Additionally, college algebra students could be tasked with determining the distances between the intersection points and the focus, enhancing their understanding of conic sections.
New Orleans teens make mathematical discovery unproven for 2,000 years - YouTube
In this engaging video, a group of teenagers from New Orleans unveil a groundbreaking mathematical discovery that challenges traditional notions held for millennia.
Scientists Just Discovered A New Formula For Pi Accidentally - YouTube
This intriguing video explores an accidental discovery by scientists who stumbled upon a new formula for Pi, revealing the delightful surprises that mathematics can hold.
Now, if you're interested in delving deeper into this subject, consider checking out my math book available on Amazon at an affordable price.
Points, Lines, and Conic Sections: A Sequel to College Algebra
Buy Points, Lines, and Conic Sections: A Sequel to College Algebra on Amazon.com ? FREE SHIPPING on qualified orders
www.amazon.com
Thank you for taking the time to read my insights.