Gauss's Theorema Egregium

The Theorema Egregium, or Awesome Theorem, was established by Gauss in 1827. This theorem states that the intrinsic geometry, specifically the Gaussian curvature of a surface, can be determined solely from its metric properties, which include distances, angles, and areas, without any need to reference the surrounding space in which the surface exists.

In simpler terms, it asserts that:

• “The Gaussian curvature of a surface remains unchanged when the surface is bent without stretching.”
• “Gaussian curvature is an intrinsic characteristic of a surface.”

Understanding Gaussian Curvature

In the realm of differential geometry, Gaussian curvature (K) at a point on a surface is defined as the product of the two principal curvatures, ?1 (maximum) and ?2 (minimum), at that point. These curvatures represent the extreme bending of the surface in two orthogonal directions.

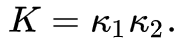
Gaussian curvature serves as a measure of a surface's intrinsic curvature, independent of its representation or the space it occupies. It can take on positive, negative, or zero values based on the surface's shape:

• Zero Gaussian Curvature: Indicates a locally flat surface, such as a plane or cylinder.
• Positive Gaussian Curvature: Found on surfaces that bulge outward, like spheres.
• Negative Gaussian Curvature: Characteristic of surfaces that curve inward, such as saddles.

To visualize, consider a flat sheet of paper; it has a Gaussian curvature of zero. When folded into a cylinder, it retains a zero Gaussian curvature overall, combining both curvatures in different directions. In contrast, a sphere exhibits positive Gaussian curvature, while a saddle shows negative curvature.

Further Insights into Gaussian Curvature

Gaussian curvature also classifies surfaces based on their curvature values:

• Developable Surfaces: Constant zero Gaussian curvature, exhibiting Euclidean geometry.
• Spherical Geometry: Constant positive Gaussian curvature.
• Pseudospherical Surfaces: Constant negative Gaussian curvature, indicative of hyperbolic geometry.

As Gauss eloquently stated, “Arc, amplitude, and curvature maintain a relationship akin to time, motion, and velocity, or volume, mass, and density.” The ramifications of this theorem are vast, marking it as a foundational result in differential geometry, which studies curved surfaces. It is essential to Riemannian geometry, the mathematical framework underpinning Einstein’s theory of general relativity.

The theorem posits that one cannot fold a flat piece of paper into a sphere without creating creases, and similarly, a sphere cannot be flattened onto a plane without altering distances. This principle holds significant relevance in cartography, as it illustrates the impossibility of creating a perfect flat map of the Earth, where every projection will inherently distort some aspects.

This theorem emphasizes the trade-off between maintaining accurate angles versus preserving distances and areas in cartographic representations. A flat map cannot simultaneously represent both accurately, underscoring the necessity of a globe for true representation.

Gauss's theorem even finds an application in a popular pizza-eating technique. A flat slice of pizza, with a constant Gaussian curvature of 0, can be gently bent while maintaining its shape, allowing for easier consumption without mess.

Gauss developed this theorem while expanding the boundaries of geometry beyond Euclidean definitions. Although he coined the term “Non-Euclidean Geometry,” he opted not to publicize his findings due to anticipated backlash, expressing his concerns to Bessel in 1829 about the potential criticism he might face.

Thank you for taking the time to read this exploration. I welcome any comments, thoughts, or suggestions you may have!

The first video, titled "Differential Geometry: Lecture 20 part 2: Gauss' Awesome Theorem," delves deeper into Gauss's theorem and its mathematical implications.

The second video, "Gauss's Divergence Theorem," provides insights into related concepts in differential geometry.