Chapter 1: Introduction to the Math Challenge

Kudos to the brave participants of our second Math Game this week! Here are the results:

1st Place: David Carnochan - 7 Points 🎉

2nd Place: Raveesh Sharma - 5 Points 🎉

3rd Place: William Keens - 3 Points 🎉

Other Participants: Neil Faver, Alfredo Esposito, ALQ, Jonathan Lynn Harvey - 1 Point each 🎉

Here’s the Solution 🔍

To tackle this problem, it’s essential to visualize the information presented through a diagram. Our goal is to move from Point A to Point B. One potential route involves traveling 135° east along the equator, followed by a 45° journey north.

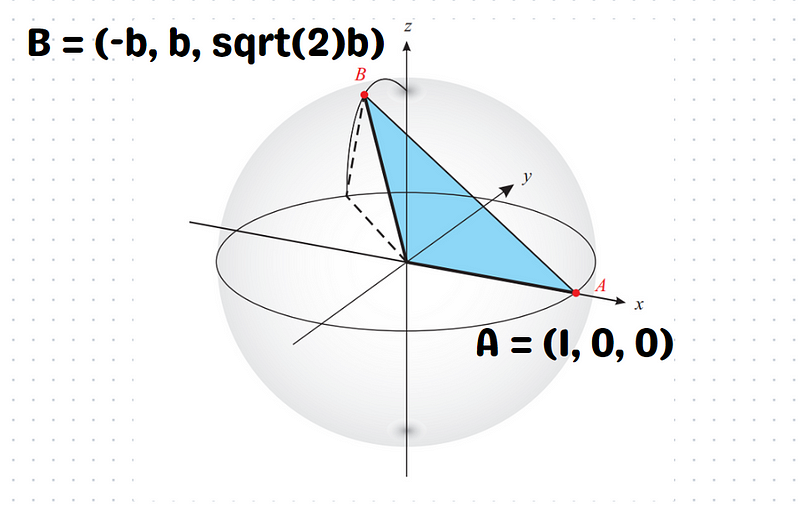
We can establish a three-dimensional coordinate system with the origin at the center of the Earth (C). Here, the positive x-axis extends through Point A, the positive y-axis intersects the equator at 160° west longitude, and the positive z-axis points toward the North Pole. The Earth's radius is set to 1.

The coordinates of Point A = (1, 0, 0) are straightforward. Now, let's determine the coordinates of Point B. We'll denote the y-coordinate of B as b. Remember, moving from A to B involves circling 135° east along the equator before heading 45° north.

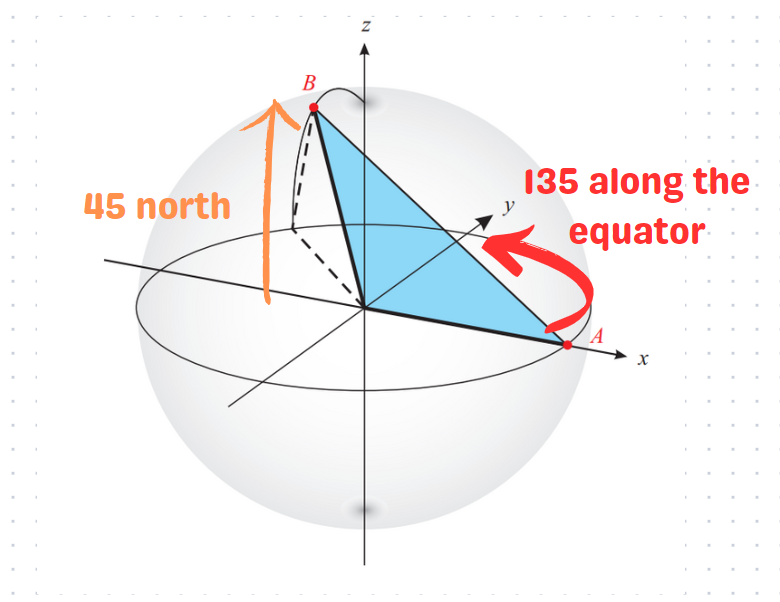
The equator corresponds to the circle on the x-y plane, while moving north translates to ascending along the z-axis.

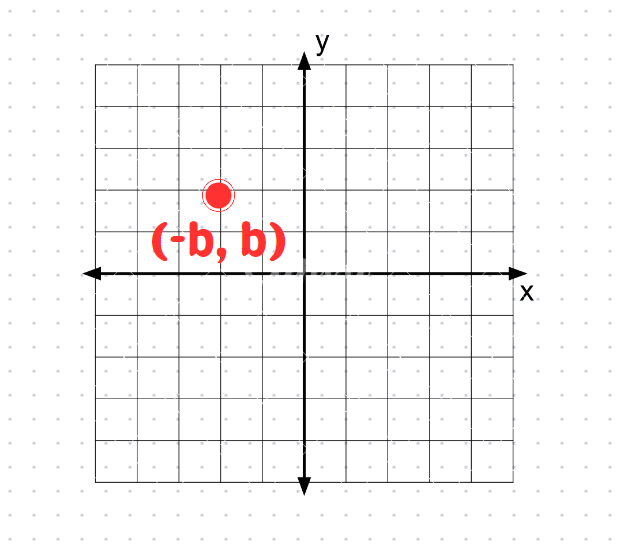
Calculating: 180° - 135° = 45°. This detail is key, as it indicates that on the x-y plane, the point is positioned on the line y = -x.

Now that we have the x and y coordinates, our next step is to determine the z-coordinate for Point B. Given that the radius of the sphere is 1 and the angle that the line segment BO makes with the x-y plane is 45 degrees, we can visualize an isosceles triangle with equal sides of length √(b² + b²) = √2b.

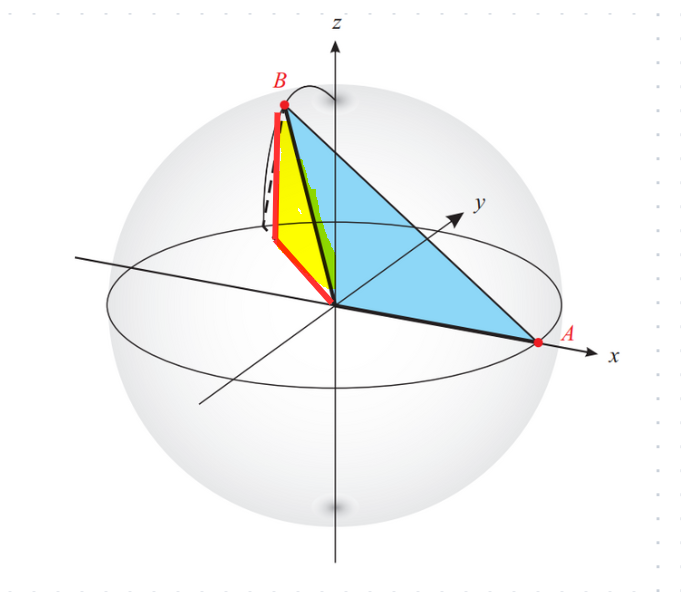
This yellow triangle illustrates our focus. Since the two red sides of the triangle are equal, the z-coordinate will be √2b.

Thus, we have the coordinates (x, y, z) = (-b, b, √2b). The equation for the sphere is x² + y² + z² = 1², allowing us to compute the value of b below.

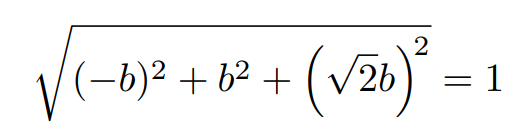
Consequently, we find b = 1/2, leading us to the coordinates (x, y, z) = (-1/2, 1/2, √2/2). Let's overlay this information onto the diagram.

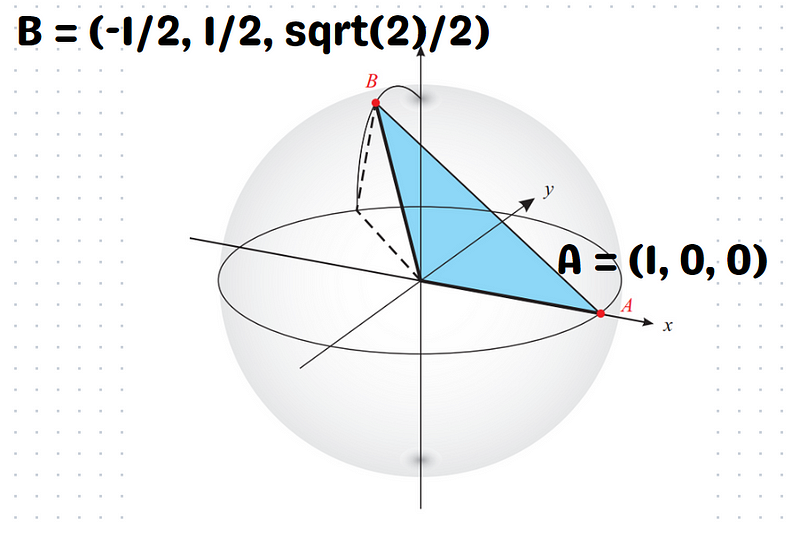
Next, we can apply the distance formula to compute the length of segment AB.

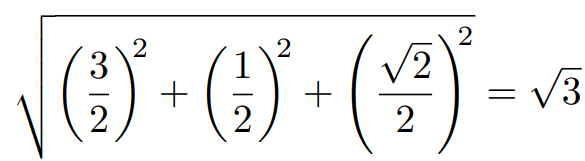
Finally, to derive the angle ACB, we will employ the law of cosines.

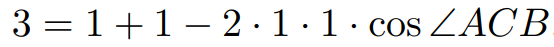
Thus, the final answer is obtained.

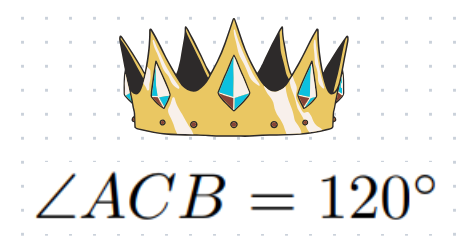
How did you fare in this week’s Math Games? We look forward to seeing you next week, Challengers! 🎉

Supporting the Math Games truly makes a difference, Challengers!

Chapter 2: Exploring Central Angles

In this chapter, we'll delve deeper into the calculations for central angles between two geographic points.

This video explains the concept of angles between two points defined by their latitude and longitude, providing a visual perspective on geographic calculations.

Here, we will learn how to use arc length and latitude to estimate the distance between two cities, demonstrating practical applications of geometry in real-world scenarios.